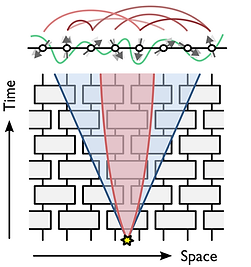
Quantum Many-Body Dynamics
What are the universal signatures of strongly-interacting quantum many-body dynamics? How does an arbitrary quantum many-body system, with generic interactions among a vast number of degrees of freedom, relax toward thermal equilibrium? How is quantum information scrambled in this process and can those scrambling dynamics be harnessed for fault-tolerant computing? From microscopic unitary evolution, by what mechanisms do thermodynamics and hydrodynamics emerge at the macroscopic scale? And how can we characterize and understand quantum many-body chaos?
The goal of this research programme is to identify the universal hallmarks of generic quantum many-body dynamics. These systems are fundamentally important yet notoriously difficult to analyse owing to their strong many-body interactions. This field sits at the frontier of multiple disciplines, bridging statistical mechanics, quantum information and complexity theory, quantum gravity and black hole physics, and revealing surprising ties to number theory. Our theoretical insights will inform experiments on near-term quantum simulators and quantum computers, providing concrete diagnostics for thermalization, entanglement growth, information scrambling and emergent hydrodynamics.